In the previous post, We had discussed about the importance of tokenization and a couple of general methods to tokenize and their merits and demerits. In this post, we will discuss about some of the approaches of tokenization. This post will include the following tokenization techniques:

1. Subword Tokenization
2. Byte Pair Encoding
3. Probabilistic Subword Tokenization
4. Unigram Subword Tokenization
5. WordPiece

1. Subword Tokenization

As discussed in the first part, the problem with the word level tokenization was that it suffers the Unknown Token problem. But, it was comparatively space efficient as we needed to store the unique words in our vocabulary and tokenizing the texts gave out less number of tokens. On the other hand, the character level tokenizer performed really well on the Unknown Token problem. This is because the characters were tokenized and any word can be formed by merging the characters. But, it faced the problem of requirement of space. Due to the method of tokenization, it generates a large number of tokens which makes it difficult to store for a large amount of text. So, to overcome this, a hybrid method is used called Subword Tokenization.

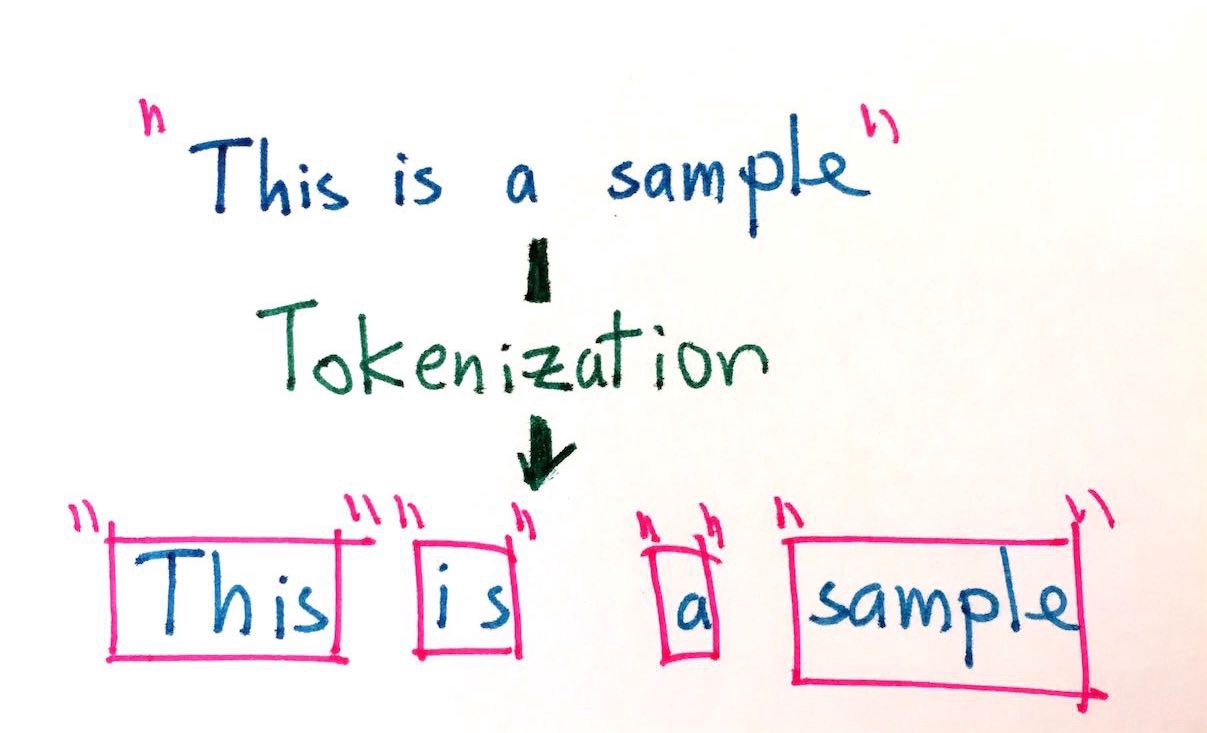
Just as the name suggests, this tokenizer works on the sub-word level. In other words, this means that instead of tokenizing based on characters, it tokenizes the words in a text into smaller tokens. As an example of this, consider the word "incompatible". If the tokenization was word based, it would generate one token, that is the word itself. The character level tokenizer would tokenize this on the character level. But, the Subword tokenizer will tokenize this word into smaller tokens like:

<in>   <comp>   <at>   <i>   <ble>

The advantage of this will be that words which are out of the vocabulary can be created by combining the tokens in the vocabulary. For example, we can generate the word "compatible" from the above tokens by joining different tokens. This will save the model from the unknown tokens problem in case of smaller vocabulary. This will also reduce the resources requirement because the number of tokens generated in this method is comparatively less than the character level tokenization. It will also save us from the extra computation required to break the text into characters. But in this method too, the problem of different methods of representation persists. We can tokenize a word into subwords in different manners than shown above.

2. Byte Pair Encoding

This is a popular algorithm for subword tokenization. Byte Pair Encoding (referred as BPE hereon) was originally introduced as a data compression technique. Let us go through the algorithm in detail. Let our sample corpus be as follows,

"deep learning enables the machines to do wonders"

The first step in this is to tokenize the text based on words. Each word is then appended with a special token to denote the end of word. By convention, this token is taken as </w>. We also will store the frequencies of the words along with the words. If we apply this step to our corpus, the frequency distribution table after the first step will be

Word count for the test corpus

Token	Frequency	Token	Frequency
deep</w>	1	machines</w>	1
learning</w>	1	to</w>	1
enables</w>	1	do</w>	1
the</w>	1	wonders</w>	1

This will be our initial token frequency distribution. The next step will include finding the character level frequency. The following table shows the character level frequency for the corpus. Note that </w> is also considered as a character now.

Character count for the test corpus

Character	Frequency	Character	Frequency	Character	Frequency
d	3	n	5	h	2
e	8	i	2	m	1
p	1	g	1	c	1
l	2	b	1	o	3
a	3	s	3	w	1
r	2	t	2	</w>	8

The above table shows the character level frequency of our test corpus. Now, the next step in the algorithm is termed as Merging. What this step does is it finds the most common (frequent) character pair from the word tokens and appends that pair as a token in the character level frequency distribution. The corresponding character's frequency is also updated during this step. For our example, the character pair "de" appears twice as a character pair in the word level tokens, once in the word "deep" and the other in the word "wonders". Thus, we will add this token in the character level table and decrease the frequency of d and e by 2. Thus, the new character level frequency distribution will be

Character count for the test corpus

Character	Frequency	Character	Frequency	Character	Frequency	Character	Frequency
d	3-2=1	n	5	h	2	de	2
e	8-2=6	i	2	m	1
p	1	g	1	c	1
l	2	b	1	o	3
a	3	s	3	w	1
r	2	t	2	</w>	8

Similarly, there are other character pairs like "s</w>" and "le" (there are more) also appears twice. They will be updated in the table in the same iteration. This procedure is called as Merging. The same procedure will continue in the next iteration also. But in the next iteration, the tokens "de", "s</w>" and others will be considered as one character in the word level tokens.

Here, there will be one question. What will happen after a large number of iterations?
After a large number of iterations, the character level token table will look something like this

Final character level token list

Token	Frequency	Token	Frequency
deep</w>	1	machines</w>	1
learning</w>	1	to</w>	1
enables</w>	1	do</w>	1
the</w>	1	wonders</w>	1

Does this look familiar? Yes. This is the same list as the word level tokens. Thus, if we run this algorithm for a large number of iterations, we will get the final token list as the same word token list in the beginning. So, how is this helpful? Generally, we run this algorithm only for a specified number of iterations. We will first decide the maximum number of tokens required and then run the algorithm until we reach the threshold.

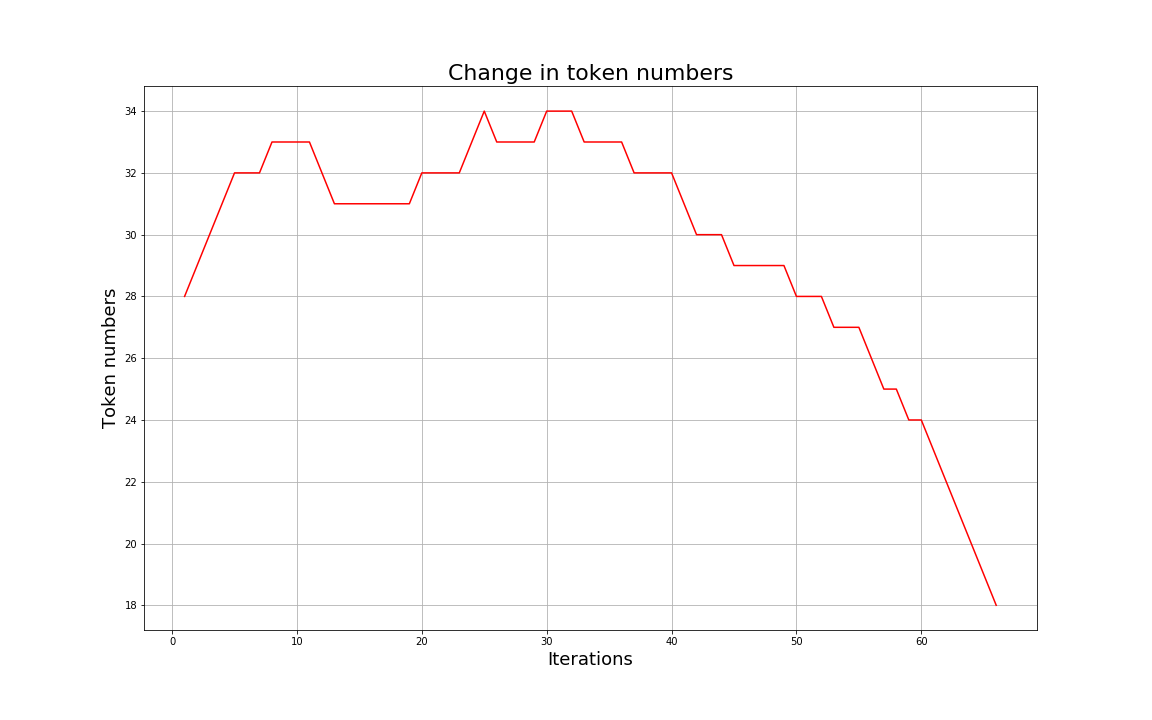
Another question which arises is that here we saw that the number of tokens in the character level list increased during the first iteration by adding the character pair tokens. But this method is to be used for data compression. So how does this justify this? The answer to this is that typically, the number of tokens will increase only for the first few iterations after which the number of tokens will gradually decrease. The following figure shows the frequency graph of a sample run of the algorithm. Please note that the graph is a sample and does not denote the run on our test corpus

3. Probabilistic Subword Tokenization

The BPE approach used the frequency of the character pairs to decide the next entry of the table. Thus, the most common words will be represented as single tokens in this method. A potential problem with this is that the final token list can be ambiguous. We can get different final tokens list with different size of corpus. If we add a sentence to our test corpus, or remove a sentence, then the final token list will not be the same. Moreover, it will also make different possible combinations for encoding a particular word. For example, take the following final token list

Final character level token list

Token	Frequency	Token	Frequency
de	5	ep	3
ee	4	e	4
d	5
p	2

If we want to encode the word "deep" using this token list, we will have multiple ways of encoding like

Encoding Methods

Encoding

de / ep

d / ee / p

d / e / ep

d / e / e / p

This is a problem similar to the word level tokenization. This problem may lead to generation of different embeddings which in turn may reduce the accuracy of the model. To counter this, a modification is made to this method. This modification leads to the introduction of Probabilistic Subword Tokenization such as Unigram Subword Tokenization.

4. Unigram Subword Tokenization

As discussed in the above point, in the Subword Tokenization method, we do not have a measure of predicting which particular token is more likely to be the best one. The Unigram method deals with the probability of a particular token than considering just the most frequent token. This method is discussed in this paper.
The Unigram model makes an assumption that each subword occurs independently. Thus, the probability of a subword sequence (this is referring to the sequences for "deep" in the previous table) can be calculated using the product of probability of each of the subwords ("d", "de", "ep" or any other). I you love mathematics, then mathematically,
let X = (x₁, x₂, x₃, x₄, .... , x_n) be the subword sequence where x_i denotes the i^th subword.
The probability of this subword sequence can be denoted as

where V (Nu) is the predefined vocabulary of tokens

The most probable segmentation is then given by

where S(X) is the set of probable subword sequence candidates

Here, the x* is obtained using the Viterbi Algorithm discussed in the paper Andrew Viterbi. 1967. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE transactions on Information Theory 13(2):260–269.

If the vocabulary V (Nu) is given, then the probability p(x_i) can be obtained by maximizing the marginal likelihood L which is given by

or

Here, D is the number of candidates for the subword sequence and S(X) is the set of the candidate sequences. This method is also termed as the EM algorithm.

In the real setting, the vocabulary V (Nu) is not available. For this, we apply the following iterative algorithm:

1. Heuristically find the vocabulary of a reasonable size from the corpus
2. Repeat the following steps till the size of vocabulary reaches the maximum decided threshold:
1. Fix the vocabulary and find the optimum p(x) using the EM algorithm
2. Compute the loss_i for each subwords where loss_i represents how likely the likelihood L is reduced when the subword x_i is removed from the current vocabulary.
3. Sort the symbols by loss_i and keep top η % of subwords (η is 10, for example). Note that we always keep the subwords consisting of a single character to avoid out-of-vocabulary.

5. WordPiece

WordPiece is a popular tokenization method which works on probabilistic methods. WordPiece can be considered as a mix of both BPE as well as the Unigram Tokenization. If we recall the process of BPE, it used to consider the most frequent character pair token in each iteration. While, the Unigram method used to consider the probability of the subword sequence. On the other hand, in each iterative step, WordPiece considers the character pair which will lead to the largest increase in the likelihood once merged. This can be calculated by subtracting the probability of the new merged pair with the sum of the probabilit of individual characters in the merged pair. Thus, for an example, the likelihood of the pair "de" is probability of "de" minus the sum of probability of "d" and probability of "e" individually. Thus, WordPiece is different from the Unigram model as it is a Greedy approach.

Thus, from this two-part article on tokenizers, we discussed about the importance of tokenization and some of its approaches. Please do let me know about your feedback on these articles and how shall I improve further. Your feedback is really important for me. Please do share this article using the buttons provided below. In further posts, I shall be talking about Positional Embedding, which is a popular way of expressing the position of a token in a sequence using a vector. Until then, have a great time!