So far in the NLP section of the blog, we have discussed about the types of tokenizers and some of its methods in this post. This article will walk you through the smallest details of a popular word representation technique called Positional Embeddings.

Introduction

The Transformers architecture was proposed as a purely attention based sequence to sequence model. Due to its ability of processing the text parallely and its advantage of solving the long sequence dependency problem of RNNs, this architecture has become very popular among researchers for performance improvements. There are many open-source implementations of transformers and its variations which have made it very easy to implement such complex architectures with just several lines of code. Due to this, it has made a very high level abstraction of this architecture and hence, the details are often ignored. I will be writing a separate article about these architectures, but this article discusses about a special part of the architecture, which is the Positional Embeddings.

What are Positional Embeddings? Is there really a need?

To understand the requirement of Positional Embeddings, it is necessary to understand the working principle of the Transformers Architecture. The transformers architecture works on a mechanism called "Attention". Not going into more details, you may picture attention as its actual meaning. In short, Attention enables the model to decide which word (or rather I should say token) in the sequence is most important and which is least. Let us take an example to understand this. Consider the situation where you are provided with a task of describing the following image

So. What do you see in this image? Your answer would be something like, "A beautiful scene of waterfalls and a lake with the background of mountains". Right? So what did you actually do while describing the image? When you wrote about the waterfalls, there were other entities in the image too. But you paid more "attention" to the waterfalls. Similarly, while writing about the mountains, you paid less attention to the lake. A similar strategy is developed using this architecture to focus on specific important words for a given sequence to sequence task. I will cover the topic of attention in detail in further posts but for this post, this intuition will suffice.

So, instead of processing the text sequentially like RNNs, Transformers adopt the attention mechanism for their tasks. But now, as there is no sequence, the model will not be able to capture the information about the position of the particular word it is processing. So, even though the longer dependencies can be handled, the architecture might miss the sense of order in the sequence of tokens. Due to this, a special word representation was introduced called Positional Embedding. Logically, it is similar to word representation like Word Embeddings. But here, only the information about the position of the token is captured. No semantic or syntactic information is included in this representation.

Now, let me ask you a question. Can you tell me a way of representing the tokens to denote the position? Remember here that we need only the position information and no other information is required. I think you have got the answer. We can assign numbers from starting from 1 to the length of the sequence to each tokens. Right? But can you think of a disadvantage of this method? A big disadvantage of using this will be that if the sequence length is big, we will get very large positional embeddings and it may dominate over other values. So, can you think of any other idea? What if we consider using numbers between 0 and 1? We will crunch the index of the token and bring it in the range [0,1], 0 being the first index and 1 being the last. Will it work fine? No. A disadvantage of this will be that we will get different embeddings for different sequence lengths. In other words, for two sequences of different lengths, the corresponding indiced token representation will not match. This should not be so. The first token in any sequence should have the same embedding value (as it denotes the position) and so is the same with the remaining tokens. So, what can be the solution to this. Instead of randomly guessing functions to represent positions, let us first define the criteria that a positional function should satisfy. We can then generate a function which satisfies all the criteria. Ideally, a positional function should satisfy the following criteria,

1. It should output a unique encoding for each sequencial token. So, the first token in any sequence will have same embedding. The second token will have same embeddings irrespective of the token or the sequence length and so on.
2. Distance between any two tokens should be same irrespective of the length of the sequence. Thus, difference between the first and second token for a sequence length of 5 should be same as the difference between the first and second token with a sequence of length 100.
3. The values of the function should be bounded. So, using 1,2,3,... and so on will not work for long sequences.
4. It must be deterministic. This means that the function should generate a determined value for a given input. It should not give output as a random number.

Sinusoidal Function

The proposed function for the positional embeddings satisfies all these characteristics. Moreover, instead of generating a scalar number as the encoding, the function gives out an N-dimensional Vector, similar to the Word Embeddings. This is because we can conveniently merge the information of the Positional Embeddings with the Word Embeddings. This function is the Sinusoidal Function. Mathematically, sinusoidal function can be described as belows
Let t be the required position in the sequence whose positional embedding vector is denoted by , which is a d dimensional vector of real numbers. Thus, in a sequence of a given length, the embedding vector of the t^th token can be pictured in the form

Let denote the i^th value in , then the Sinusoidal Function can be defined as

Where,

So, it can be established from the formula that in the vector, the even indexed position (indexing starts from 0) uses the sine function and the odd indexed position uses the cosine function. In the form of a vector, it can be shown as follows

Not able to Visualize? Read On!

Assuming that you are well aware of the Sine and the Cosine functions, the term denotes the frequency of the Sine or the Cosine wave. So, with the decrease in the value of , the wavelength of the wave will increase and vice versa. Here is a small comparison

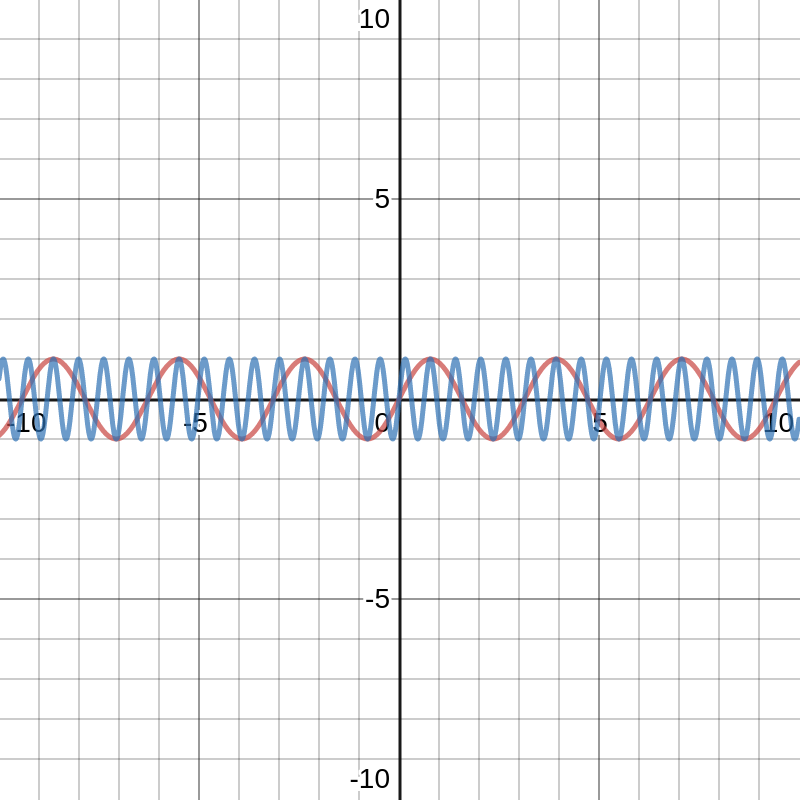
Here, the red graph is for sin(2t) and the blue one is for sin(10t). Similar happens the situation for cosine. So, now, here we have a vector of various sine and cosine values with different values of . So, if you visualize roughly, it will be a lot of wavy figures on a plane. Just like the picture which is shown as the header image of this post. Let me insert it here once again so you do not need to keep scrolling

A similar situation is created for a sequence of tokens. To get the embedding for the i^th token, we take the values obtained from each wave at x=i and arrange the values in a vector. As visible in the legend of the graph above, the dimensions of the vector are marked. This shall prove to be a good visualization for the encodings.

One more Question?

This may lead us to one more question. Why do we use Sine as well as Cosine functions. Why not only Sine or only Cosine? This is because Sinusoidal Function has a very interesting characteristic which will turn out to be useful for our cause which Sine or Cosine functions alone can not fulfill. This is the characteristic of Relative Positioning. This means that for a given positional embedding of a position pos, we can determine the positional embedding for a position pos+k as a linear function of the positional embedding of position pos. Let us prove this statement as well.

As we know that a linear function is of the form , let us try to formulate such a function for the positional embeddings. for a given position , we need to find the embedding for position . For the sake of simplicity, we will consider the dimension of the embedding as 2. As the positional embedding is a matrix, we will get a function like

where is a matrix which we need to find and is the Positional Embedding matrix. This matrix should not depend on any variable other than .

So, let us replace the variables in the above formula with the real values. The linear formula will look like

Continuing this, we can understand that the matrix M will be a 2x2 matrix. Thus, replacing the value of M,

Now, as you are already aware of the Addition Law in Sine and Cosine functions, and , solving further, we will have

Comparing the corresponding rows, we get

As we can observe here, the matrix is independent of any other variable than . This could not have been achieved if we would have used only Sine or only Cosine functions.

This sums up most of the details of the Positional Embeddings and the Sinusoidal Function. Below are the explanations of some questions which you might still have regarding the embeddings and the sinusoidal function.

1. How are the Positional Embeddings used?

The Positional Embeddings can be used in two ways. One way is that they can be concatenated along with the Word Embeddings and given as an input to the architecture. But this is not the way they are actually used. The other way is to add the positional embeddings to the word embeddings. Due to this, the dimension of the positional embedding vectors are set equal to the dimension of the word embedding vectors. Why is it so? Why is addition preferred over concatenation? To answer this, let us consider this example. Consider a sequence S. We select two tokens of the sequence A and B. Let x and y be the word embeddings for the tokens A and B respectively. Let a and b be the positional embeddings for the tokens A and B respectively. Now, to calculate the attention, we take the dot product of the Query vector of one token with the key of the other token (I will have to be a bit technical here to complete the answer). Let Q be the Query weight matrix and K be the key weight matrix. Thus, we need to find (Qx)'(Ky) here. This is equivalent to finding x'(Q'K)y according to the rules of transpose multiplication. So, basically the important term here is (Q'K) which decides the amount of attention the model gives to a particular token. Thus, the term x'(Q'K)y denotes how much attention the token x (more specifically A) need to be given for the token y. Now, let us say we are adding the positional embeddings to the word embeddings. Now, the attention will become (Q(x+a))'(K(y+b)). Expanding this, we will get the term (Qx)'(Ky) + (Qx)'(Kb) + (Qa)'(Ky) + (Qa)'(Kb). This term expanded further will give us x'(Q'K)y + x'(Q'K)b + a'(Q'K)y + a'(Q'K)b. SO, along with answering the actual question of how much attention the token x need to be given for the token y, it also answers thre more questions about how much attention the position of the token x (more specifically A) need to be given the position of token y, how much attention the position of the token x (more specifically A) need to be given for the token y and how much attention the token x (more specifically A) need to be given the position of token y. This would not have been possible if the embeddings were concatenated instead.

2. Why '10000'?

The number 10000 used in the frequency is actually for taking a large number there. Taking a large number in the denominator of the frequency will increase the wavelength of the wave. And as we know that for a number of given waves, the values of the waves will repeat at the LCM of the wavelength. Thus, if we keep a very high wavelength, the LCM will be high and the values of the embeddings will not repeat until a long time. This will facilitate the usage of larger sequences in our architectures. Thus, 10000 is used in the frequency.

So, this was all the details about the Positional Embeddings. Please do share this article if you liked the content. Do let me know in case I have missed any detail or you may have a question which is unanswered here. I shall get back to you in no time. Also, do provide me some suggestions to improve the articles. It shall help me a lot. Stay tuned for the next article. Until then, have a great time!